Thermal Cycling Fatigue of a Chip Resistor Solder Joint

A physics-based narrative of damage initiation, crack propagation, and final failure supported by microstructural evidence.

January 30 2026

Ed Hare, SEM Lab. Inc.

1.  Introduction

This document describes the physical sequence of events that occur in a SN63 solder joint supporting a chip resistor during accelerated thermal cycling. The narrative integrates mechanics-based fatigue modeling with direct metallographic evidence, demonstrating how cyclic thermo-mechanical strain accumulates and ultimately produces electrical failure.

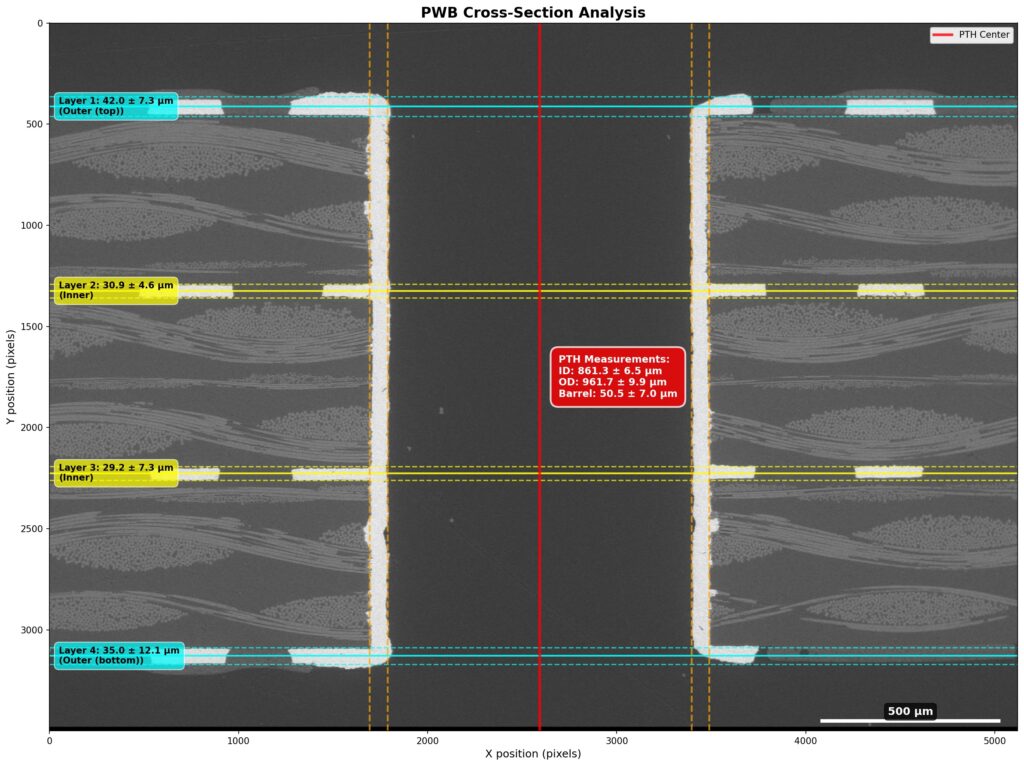
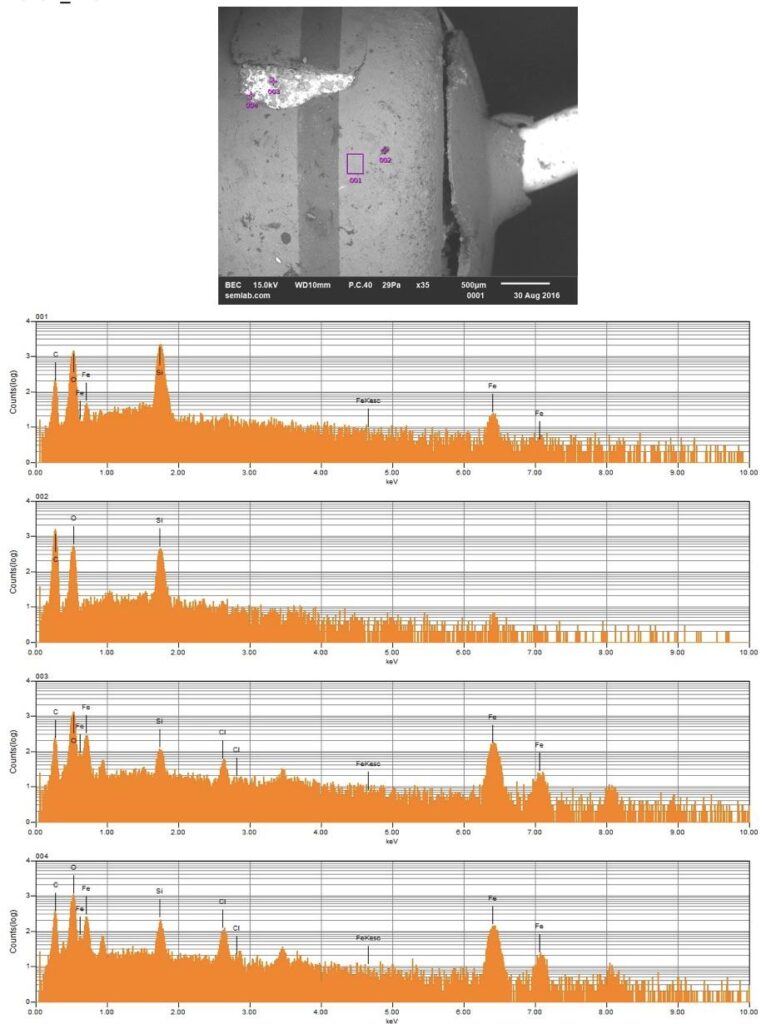
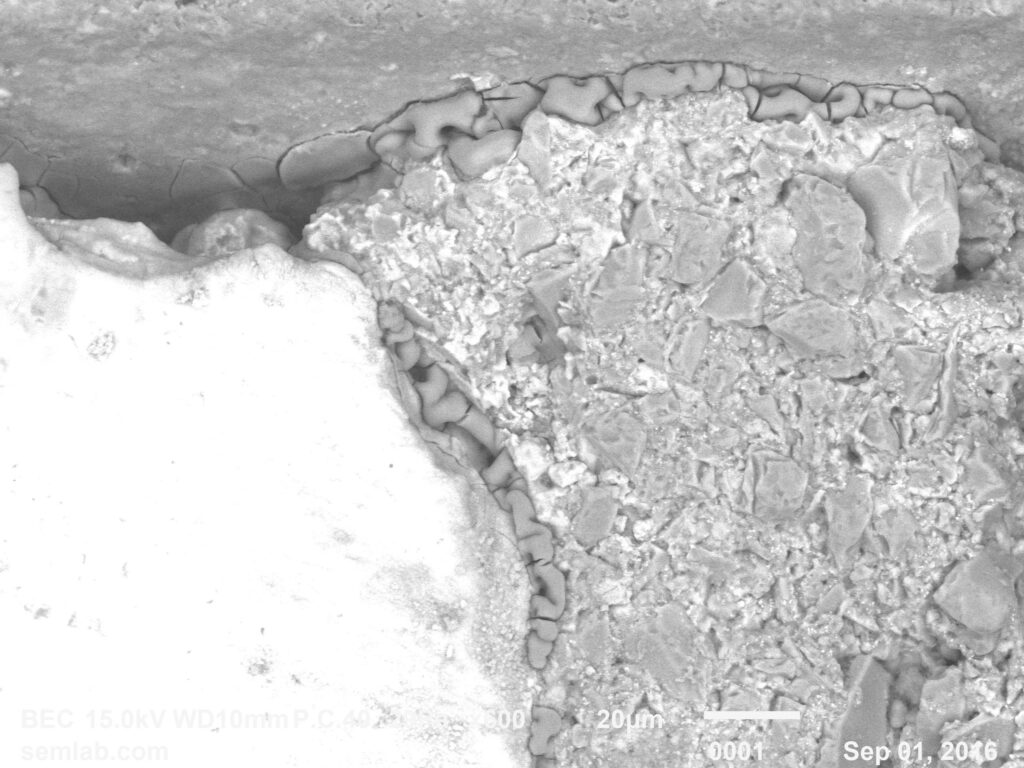
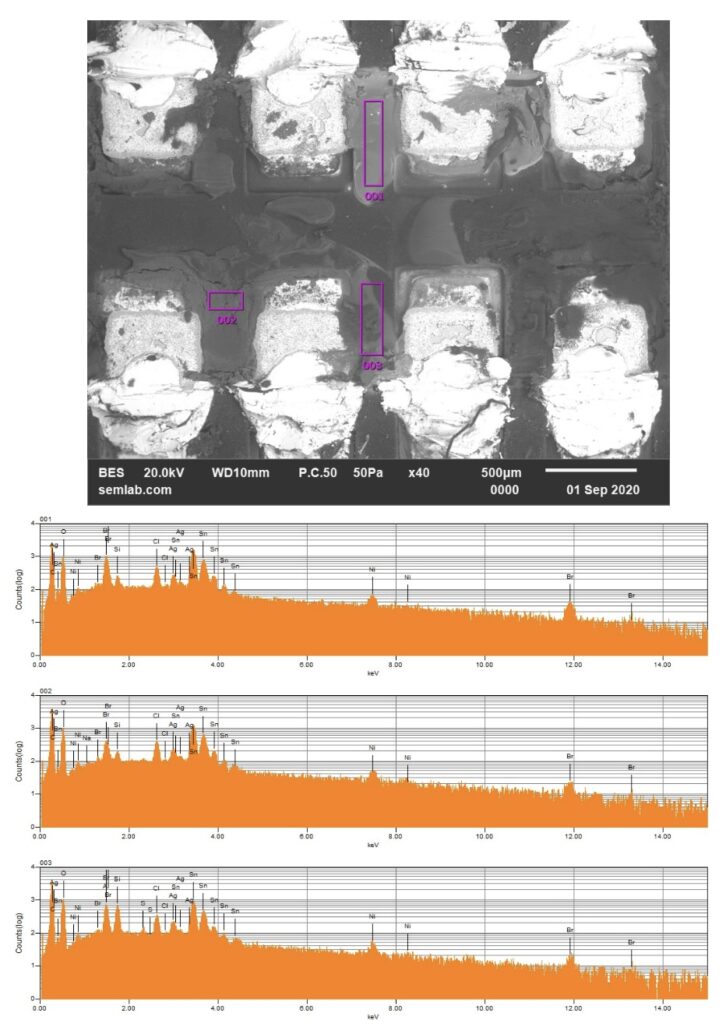
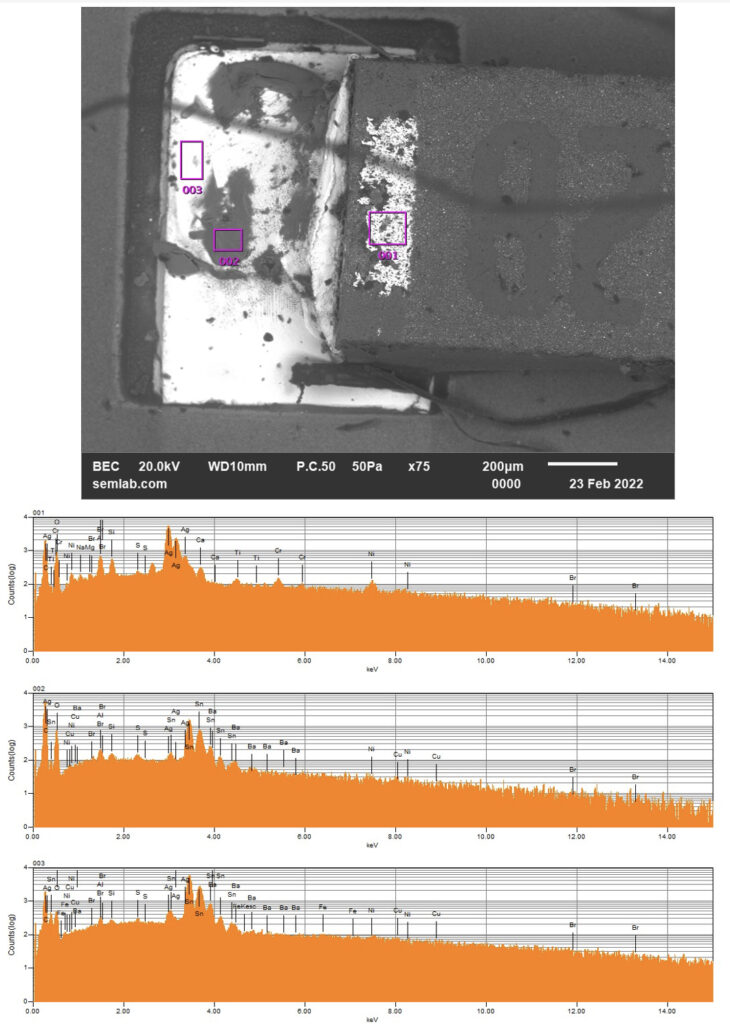
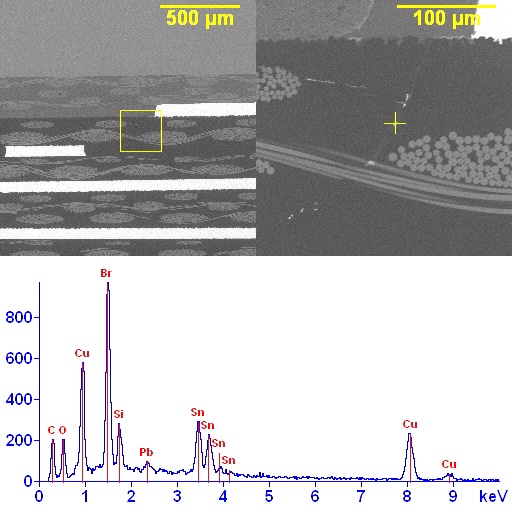
Figure 1. Cross-sectional SEM micrographs of a chip resistor solder joint: (top-left) as-assembled microsection; (top-right) global thermal fatigue fracture; (bottom-left) subsurface crack beneath termination; (bottom-right) advanced fracture within fillet.

2.  As-Assembled Condition: Geometry-Driven Strain Amplification

The as-assembled solder joint exhibits low standoff height and sharp geometric transitions at the termination edges. This geometry produces a high strain amplification factor during thermal cycling. Even under nominal workmanship conditions, the mismatch in coefficients of thermal expansion between the ceramic component, FR-4 PCB, and SN63 solder results in immediate elastic–plastic deformation during the first thermal excursion.

3.  Early Cycling: Stress Relaxation with Permanent Damage

During the high-temperature dwell portion of the thermal cycle, solder stress relaxes via creep. While peak stress decreases, plastic strain and microstructural damage are retained. Dislocation motion and grain boundary sliding irreversibly alter the solder microstructure, establishing the conditions for fatigue crack nucleation.

4.  Crack Initiation Beneath the Termination

Crack initiation occurs preferentially beneath the component termination, where constraint and shear strain are highest. At this stage, cracks are typically subsurface and electrically benign, explaining why early-life damage is rarely detected by functional testing. This regime corresponds to the low-cycle failure tail observed in fatigue life distributions.

5.  Stable Crack Propagation Driven by Inelastic Energy

With continued cycling, the crack propagates incrementally under the influence of cyclic inelastic strain energy. Each thermal cycle deposits additional plastic work at the crack tip, resulting in stable, energy-controlled growth along the solder–IMC interface and adjacent solder matrix.

6.  Final Failure: Ligament Overload and Electrical Open

As the effective load-bearing area diminishes, local strain intensifies in the remaining solder ligament. Crack growth accelerates rapidly, culminating in complete separation of the joint. Electrical failure often appears sudden, although it is the result of damage accumulated over hundreds of prior cycles.

7.  Modelling

A.  First power-up: elastic–plastic strain sets in

The very first thermal excursion from −40 °C toward 105 °C immediately imposes differential expansion between:

• the FR-4 PCB (CTE ≈ 15 ppm/°C),
• the 0603 ceramic resistor (≈ 6 ppm/°C),
• and the SN63 solder joint (≈ 23 ppm/°C).

Because the joint has a high geometric amplification factor (L/2h ≈ 15), the global CTE mismatch is converted into a large local shear strain. The total shear strain range is already ~3.9% in the very first cycle. That is well beyond purely elastic behavior — the joint yields almost immediately.

B.  Hot dwell: stress relaxes, damage does not

At the 105 °C hot dwell, the solder undergoes time-dependent creep. The peak shear stress (≈ 34 MPa) partially relaxes, falling to about 59% of peak during the dwell.

This often creates a false sense of safety — but physically:

• stress relaxation does not undo plastic strain,
• it locks in permanent microstructural damage.

Our retention metric (W_relax ≈ 0.63) shows that a large fraction of the stress cycle remains fatigue-relevant even after relaxation. In other words, the joint never “resets.”

C.  Cooling reversal: strain reverses before structure recovers

As the assembly cools back toward −40 °C, the direction of shear reverses:

• previously elongated regions are now compressed,
• previously compressed regions are now elongated.

However, the solder’s microstructure has already evolved during the hot dwell:

• dislocation density has increased,
• grain boundaries have slid,

This produces a closed hysteresis loop — the area of which is your inelastic energy proxy (W ≈ 0.79 MPa per cycle). That area is irreversible damage.

D.  Early micro-crack nucleation (order of N₁ ≈ 75 cycles)

Because strain is highest at geometric discontinuities, the first microscopic cracks form:

• at the solder-to-termination interface,
• typically near the toe of the joint where constraint is highest.

This aligns with the N₁ life (~76 cycles) predicted by the Darveaux framework:

a small percentage of joints will already have a physically detectable crack very early in life.

At this stage:

• the joint is still electrically continuous,
• resistance is unchanged,
• visual inspection usually shows nothing.

But mechanically, the failure process has started.

E.  Stable crack propagation driven by cyclic plastic work

With continued cycling:

• each hysteresis loop deposits more inelastic energy at the crack tip,
• the crack grows incrementally during each cycle,
• growth accelerates slightly as the effective load-bearing area shrinks.

This is the Darveaux propagation regime — energy-controlled, not stress-controlled.

The crack advances roughly along the solder–IMC interface or through the solder near that interface, depending on local microstructure.

Importantly:

• stress relaxation does not stop this phase,
• it only redistributes where the damage accumulates.

F.  Approach to median failure (N₅₀ ≈ 750 cycles)

By the time ~50% of joints have failed:

• the dominant crack has traversed most of the effective joint width,
• remaining ligaments carry increasing local strain,
• stiffness drops measurably.

Electrical opens may appear intermittently first (thermal-dependent opens), then permanently. This corresponds well to the Darveaux N₅₀ ≈ 759 cycles, which is the most physically grounded metric here because it is tied directly to dissipated energy.

G.  Final separation: rapid mechanical collapse

Once the crack reaches a critical length:

• only a small solder ligament remains,
• local strain skyrockets,
• fracture completes in just a few additional cycles.

The end state is a classic fatigue-separated solder joint, often with:

• a relatively flat crack face,
• IMC exposed along part of the fracture,
• minimal bulk solder necking (because creep already relieved much of the peak stress earlier).

8.  Conclusions

The combined modeling and microstructural evidence demonstrates that solder joint thermal fatigue is a progressive, geometry-driven process governed by cyclic plastic strain and inelastic energy dissipation. The provided images directly validate the predicted crack initiation sites and propagation paths, transforming abstract fatigue metrics into observable physical phenomena.

Click link to download …

Ed Hare – Consultant

We can use a BSE SEM image of a PWB microsection like this …

 

 

… and generate auto feature measurements like this in under a second.

 

 

And with a report like this …

# PWB Cross-Section Analysis Report

## Analysis Metadata
– **Report Generated:** 2025-11-12 11:04:20
– **Original Image:** NNNNNN_1.jpg
– **Magnification:** 45x
– **Scale:** 0.53542 µm/pixel
– **Image Dimensions:** 5120 x 3840 pixels (W x H)
– **Copper Coverage:** 5.6%
– **Analysis Method:** Pure Computer Vision

—

## Layer Analysis

| Layer | Y-Centerline (px) | Thickness (px) | Thickness (µm) | Std Dev (µm) | Notes |
|——-|——————-|—————-|—————-|—————|——-|
| 1 | 412 | 78.46 | 42.01 | 7.33 | Outer (top) |
| 2 | 1324 | 57.76 | 30.92 | 4.62 | Inner |
| 3 | 2226 | 54.56 | 29.21 | 7.29 | Inner |
| 4 | 3129 | 65.29 | 34.96 | 12.08 | Outer (bottom) |

## Dielectric Spacing

| Between Layers | Thickness (px) | Thickness (µm) |
|—————-|—————-|—————-|
| Layer 1 to 2 | 831 | 444.93 |
| Layer 2 to 3 | 834 | 446.54 |
| Layer 3 to 4 | 827 | 442.79 |

## PTH Geometry

| Measurement | Value (px) | Value (µm) | Std Dev (µm) |
|————————–|————|————|—————|
| Inner Diameter (ID) | 1608.6 | 861.28 | 6.50 |
| Outer Diameter (OD) | 1796.2 | 961.71 | 9.85 |
| Barrel Copper Thickness | 94.3 | 50.51 | 7.00 |
| Left Barrel | 98.2 | 52.57 | 8.67 |
| Right Barrel | 90.5 | 48.45 | 4.80 |

## Summary

– **Total layers detected:** 4
– **Outer layer thickness (avg):** 38.48 µm
– **Inner layer thickness (avg):** 30.07 µm
– **Average dielectric spacing:** 830.7 px (444.76 µm)

Contact ehare@semlab.com if you are interested in this type of tool for data collection.

Residual Molding Compound After Decapsulation

… as an Indicator of Excessive Current Flow and Joule Heating

Ed Hare – SEM Lab, Inc.

Introduction

Residual molding compound is a critical indicator of failure mode in the failure analysis of electronic components such as PMICs, SOTs, diodes, etc. This article explores how the presence of residual molding compound can signal excessive current flow, leading to charred molding compound due to joule heating. Understanding the correlation between residual molding compound and electrical overstress is an essential tool for diagnosing over current failures in electronic devices.

Background

Molding compounds are used to encapsulate semiconductor devices to protect them from environmental factors and mechanical stress. However, during the failure of electronic components, the molding compound can thermally degrade, leaving behind residual charred material after chemical decapsulation. This degradation is often a result of excessive heating caused by high current flow, known as joule heating.

Residual Molding Compound and Electrical Overstress

The presence of residual molding compound  on various parts of a device, such as bond pads, bond wires, and die surfaces, can indicate areas where overheating has occurred. Several job reports have documented the association between residual molding compound  and electrical overstress:

**Bond Pads and Die Surface **: Residual molding compound has been observed on bond pads (Fig. A) and the die surface (Fig. B). This suggests that these areas experienced significant heating, leading to the charring of the molding compound.

 

Fig. A – Processor Supervisory Circuit IC, pin-3, power-fail comparator output.

 

Fig. B – Single-Chip Microcomputer.

 

**Bond Wires**: residual molding compound on a bond wire serves as an indicator of excessive current cause overheating that is typically centered on the mid-span region of the bond wire, because the bonded ends of the wire are heat sunk and therefore cooler.

Fig. C – Voltage Regulator, TO-92 package, V_in bond wire.

 

Fig. D – Voltage Regulator, TO-92 package, V_in bond wire encrusted in residual molding compound.

 

Additional Case Studies

Some additional cases provide examples of how residual molding compound  can be used to diagnose electrical overstress:

– **Case 1**: residual molding compound  on the die surface indicated a hot spot where the molding compound was charred. This charring made the residual molding compound  resistant to the decapsulant, highlighting the severity of the overheating.

 

Fig. E – 8-bit Flash Microcontroller, associated with pin-32, an address signal.

– **Case 2**:  Residual molding compound  on the die surface suggested that the area had over-heated and carbonized the encapsulant resin, providing clear evidence of electrical overstress.

 

Fig. F – Dual SPDT Switch, optical image of residual molding compound on V+ bond wire.

 

– **Case 3**: residual molding compound adhered to a MOSFET device centered on the source wire bond and associated die region.

 

Fig. G – MOSFET device, residual molding compound at source wire bond and associated die region.

Conclusion

Residual molding compound is a valuable indicator of electrical overstress in electronic components. Its presence on bond pads, bond wires, and die surfaces suggests that these areas experienced excessive heating due to high current flow. By understanding the correlation between residual molding compound  and electrical overstress, engineers can diagnose failures more accurately and implement measures to prevent similar issues in the future.  Our future efforts include thermal modelling to potentially provide pulse width estimates based on estimated volume of residual molding compound.

SEM Lab Inc – ENIG Gold Thickness Measurement

 

… view as Slide Show

ENIG Gold Thickness

 

Resistor Corrosion Failures Associated with Flux Residues and Protective Layer Breakdown

Ed Hare – SEM Lab, Inc.

Analysis of multiple case histories shows that resistors are vulnerable to corrosion when flux residues, halide contaminants, and weak protective layers interact. These failures are not isolated anomalies; they represent a recurring set of conditions tied to assembly practices, cleaning processes, and material compatibility.

In one study, resistors exhibited rusted end caps beneath failed paint layers. Once the protective paint fractured, chloride-bearing residues penetrated and initiated corrosion at the steel end caps. This ingress path was a consistent feature across samples.

 

Figure 1 – Optical view of end-cap paint failure.

 

Backscattered SEM and EDS analysis confirmed that rust developed beneath the paint, with chlorine contamination detected in the affected regions. The presence of halides strongly implicates solder flux and cleaning residues as the root source.

 

Figure 2 – SEM/EDS of corrosion under paint layer.

 

The corrosion was not limited to the cap itself. In several cases, the attack extended to the resistive film where it joined the termination, producing variable resistance and eventual opens.

 

Figure 3 – SEM image of resistive film attack.

 

Other resistor types showed crystalline corrosion products directly on their terminations. SnO₂ crystals were identified at the surface, again associated with flux residues containing chlorine, sulfur, and phosphorus. These crystalline deposits physically bridge surfaces and act as local ionic conductors.

 

Figure 4 – Corrosion crystals on resistor termination.

 

For network packages, the failure mechanism was often contamination trapped beneath the component. SEM sections revealed a mixture of corrosion products and solder flux beneath the resistor arrays, exactly in the spaces that are inaccessible to normal cleaning. These residues were electrically active, producing leakage and shorts between adjacent signals.

 

Figure 5 – Corrosion and flux residue trapped under a resistor network.

 

Elemental analysis of the trapped material confirmed carbon, oxygen, tin, and high levels of chlorine and bromine—classic signatures of flux activators.

 

Figure 6 – EDS spectra of halide-rich residues.

 

Thick-film resistor terminations proved especially susceptible to sulfur attack. Elemental mapping showed sulfur and chlorine concentrated at the silver film layer, producing degradation of the conductive path. This highlights the material sensitivity of silver-based resistor films to environmental residues.

 

Figure 7 – Elemental map of thick-film resistor corrosion.

 

Finally, some failures were linked to process-induced damage. Secondary solder touch-up operations created fractured nickel plating and left flux residues on resistor terminations. In these cases, corrosion was not the only factor; mechanical disruption of the plating accelerated failure at the solder joint interface.

 

Figure 8 – Flux and mechanical termination damage.

⸻

Discussion

Across these case studies, a consistent theme emerges: halide contamination from flux and cleaning residues is the dominant driver of corrosion. Once protective barriers such as paint layers, solder masks, or conformal coats are compromised, chloride and sulfur species attack both the termination metallization and the resistor element itself.

The resulting damage pathways—rusted end caps, SnO₂ crystal formation, halide-rich residues under networks, sulfur attack on silver thick film, and fractured nickel plating—lead to the full range of electrical consequences: variable resistance, open circuits, leakage currents, and shorting between nodes.

Conclusion

The reliability of resistors depends not only on their intrinsic design but also on assembly and cleaning discipline. Avoidance of aggressive flux chemistries, thorough removal of ionic residues, and protection of vulnerable interfaces are critical. These cases demonstrate that when those controls are absent, resistor corrosion becomes an inevitable and costly failure mechanism.

 

Conductive anodic filament (CAF) failure has become a critical reliability concern in modern printed wiring boards (PWBs). As designs push toward finer pitch, higher layer counts, and higher operating voltages, the risk of CAF increases. CAF refers to the growth of a conductive copper filament through the glass/epoxy dielectric under bias and humidity, bridging adjacent conductors. These failures typically occur below the surface of the laminate, making them difficult to detect until electrical breakdown occurs.

 

Fig.1 – Plated copper is deep in the dielectric space between holes in the laminate.

CAF formation is often associated with copper plating extending beyond the plated through hole wall into adjacent resin-rich regions. Once copper is introduced into these dielectric pathways, bias and moisture accelerate ion migration. The resulting copper grows along glass/resin interfaces, creating hidden conductive bridges deep inside the laminate stack.

 

Fig. 2 – Failures were caused by CAF between +12V and GND at a connector.

CAF is particularly insidious when it forms between high and low potential conductors, such as +12 V and ground nets. Even small leakage currents can result in intermittent failures, system resets, or complete short circuits.

 

Fig. 3 – Resin starvation in glass bundles can cause CAF failure.

Areas where resin coverage is poor around glass bundles provide prime initiation sites. Resin starvation leaves microvoids and channels at the fiber-resin interface. These gaps act as capillaries for moisture and ionic species, establishing a pathway for CAF growth. Process controls during lamination—such as ensuring proper resin flow and glass fabric wetting are therefore crucial to prevention.

 

 

Fig. 4 – Crazing and measling of laminate can support CAF failure.

Crazing and measling are microcrack and void patterns associated with glass bundle movement or thermal-mechanical stresses. These features effectively increase the available surface area and pathways for CAF propagation. A laminate that visually shows measling may already harbor hidden weaknesses that accelerate conductive filament growth under bias and humidity stress testing.

 

Fig. 5 – Dark field optical images can be useful for examining fiber delamination in PWB sections.

Optical microscopy, particularly in dark field mode, highlights fiber pullout, voiding, and microcracking within cross-sections. These imaging techniques provide valuable insight into resin-glass integrity and delamination. Proper sectioning and imaging remain vital diagnostic steps in CAF investigations.

Conclusion

CAF originates inside the laminate microstructure, where resin-glass interfaces and plating intrusions provide pathways for copper migration. Once established, these conductive filaments undermine reliability and are difficult to detect by conventional inspection. Effective CAF prevention requires careful control of laminate fabrication, resin distribution, and design spacing rules, coupled with targeted failure analysis methods when issues arise.

 

Weibull analysis is a powerful statistical tool commonly used in electronics reliability engineering to model failure behavior over time. Its flexibility in handling different failure modes—early life, random, or wear-out—makes it especially valuable in the complex, multi-mechanism failure environments typical of electronic components and assemblies.

These are key use cases for Weibull analysis in electronics reliability:

 

 

 

1.

Failure Mode Characterization

 

 

 

• Purpose: Determine whether a failure mode is infant mortality, random, or wear-out.

• Example: Analyzing time-to-failure data for a batch of surface mount capacitors under thermal cycling to distinguish between early cracking (β < 1), random failures (β ≈ 1), or fatigue wear-out (β > 1).

 

 

 

 

2.

Life Prediction / Time-to-Failure Estimation

 

 

• Purpose: Estimate the median life or characteristic life (η) of a device under use or test conditions.

• Example: Predicting BGA solder joint fatigue life under power cycling stress based on accelerated test data.

 

 

 

 

3.

Accelerated Life Testing (ALT) and Extrapolation

 

 

• Purpose: Use high-stress data (e.g., temperature, humidity, voltage) to model life at normal use conditions using acceleration models (e.g., Arrhenius, Coffin-Manson, Norris-Landzberg).

• Example: Subjecting PCBs to elevated temperature and humidity to simulate dendritic growth or corrosion, then applying Weibull + acceleration models to estimate field failure rates.

 

 

 

 

4.

Comparative Reliability of Designs, Materials, or Processes

 

 

• Purpose: Compare different design or material variants to determine which one offers longer life or fewer failures.

• Example: Comparing ENIG vs. ENEPIG surface finishes by running temperature cycle tests and plotting separate Weibull curves to assess which has higher characteristic life.

 

 

 

 

5.

Failure Rate Estimation (λ) and MTBF Calculations

 

 

• Purpose: Derive Mean Time Between Failures (MTBF) or failure rate, especially in systems with a constant failure rate (β ≈ 1).

• Example: Estimating MTBF for a power supply module operating in a data center, where failures are largely random due to overstress or component defects.

 

 

 

 

6.

Warranty and Risk Forecasting

 

 

• Purpose: Predict percentage of devices that will fail before a specific time to define warranty coverage.

• Example: Forecasting the probability that LED driver ICs will fail within a 5-year service window in a commercial lighting application.

 

 

 

 

7.

Root Cause Correlation

 

 

• Purpose: Identify underlying mechanisms by examining how β (Weibull slope) changes with design, processing, or test variables.

• Example: If β increases significantly after a design change, it may indicate better control over early life defects.

 

 

 

 

8.

Field Return Analysis

 

 

• Purpose: Apply Weibull analysis to returned units from the field to distinguish between systemic failures and random defects.

• Example: Analysis of failed MLCCs from automotive ECUs to determine if failures are consistent with mechanical flex cracking (brittle failure, high β) or ESD-related dielectric breakdown (random).

 

 

 

 

9.

Burn-In Screening Optimization

 

 

• Purpose: Use early life Weibull data (β < 1) to justify burn-in screening duration and effectiveness.

• Example: Determining if 24-hour power-on burn-in is sufficient to weed out early IC failures caused by latent defects.

 

 

 

 

 

10.

Reliability Growth Tracking

 

 

• Purpose: Show how process improvements (e.g., cleaning, soldering controls, layout changes) shift the Weibull distribution toward higher reliability.

• Example: Tracking Weibull parameters of conformal-coated PCBs before and after changing flux chemistry or cleaning method.

 

 

We can write equations and make calculations based on atomic weight & density of pure elements to determine what volume change (%) occurs when for example Au + 4Sn >>> AuSn4 and using intermetallic densities from published sources as shown in Fig. A.

Fig. A – Volume change during formation of solder intermetallic compounds.

Since volume changes during IMC formation, we can expect void formation and interfacial cracking at the IMC/matrix interface as most of these systems show contractions in volume. This may be a contributing factor to thermal fatigue damage found in solder joints on printed circuit board assemblies.

The melting temperature of these intermetallic compounds are shown in Fig. B.  Most of these melting temperatures are greater than peak reflow temperature, so the IMCs exist as solid particles in molten solder until the system cools below the solidus temperature.

Fig. B – Melting temperature of intermetallic compounds.